সরলরেখার ঢাল
একটি সরলরেখা X অক্ষের সাথে ধনাত্মক দিকে যে কোণ উৎপন্ন করে, তার ত্রিকোণমিতিক tan-কে ওই সরলরেখার ঢাল বলে। অধ্যাপক আর. জি. লিপসি (R. G. Lipsey) বলেন, “একটি সরলরেখার ঢাল হলো X অক্ষ বরাবর দূরত্ব পরিবর্তন ও Y অক্ষ বরাবর দূরত্ব পরিবর্তনের অনুপাত।” (The slope of a straight line is the rating of the distance moved up the Y-axis to the distance moved along the X-axis.)
সরলরেখার ঢাল নির্ণয়ের সূত্রটি হলো-
সরলরেখার ঢাল = লম্ব দূরত্ব/আনুভূমিক দূরত্ব
= Y অক্ষ বরাবর দূরত্ব পরিবর্তন/X অক্ষ বরাবর দূরত্ব পরিবর্তন
= BC/AC [ চিত্রে প্রদর্শিত ]
| ঢাল কাকে বলে | ঢাল নির্ণয়ের সূত্র | রেখার ঢাল কি ও নির্ণয়ের সূত্র |
ধনাত্মক ঢাল
কোনো অপেক্ষক একমাত্রার হলে সংশ্লিষ্ট রেখা সরল আকৃতির হয়। মনে করি, একটি একমাত্রার যোগান অপেক্ষক y = -a + d(x) হতে AB অঙ্কন করা হয়েছে। এখন AB সরলরেখার ঢাল নির্ণয় করতে হবে।
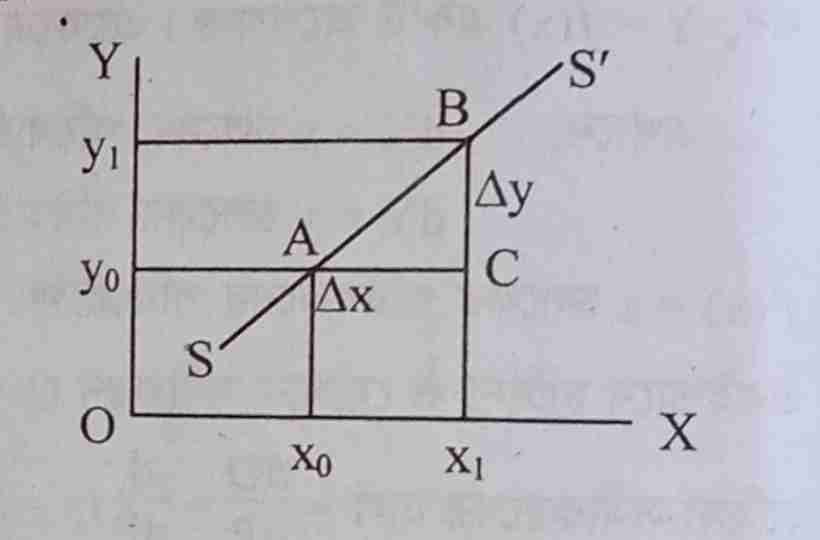
মনে করি, SS’ রেখার ওপর A বিন্দুতে X ও Y এর প্রাথমিক পরিমাণ যথাক্রমে Xo ও Yo ছিল। পরবর্তীতে X ও Y এর পরিমাণ বৃদ্ধি পেয়ে যথাক্রমে X1 ও Y1 হয়, যা B বিন্দুতে দেখানো হয়। সুতরাং SS’ রেখার উপরিস্থিত A ও B বিন্দুদ্বয়ের স্থানাঙ্ক যথাক্রমে (Xo, Yo) এবং (X1, Y1) হয়।
∴ AC = X1 – Xo = Δx এবং BC = Y1-Yo = Δу
| ধ্রুবক কাকে বলে | চলক ও ধ্রুবকের মধ্যে পার্থক্য |
ঋণাত্মক ঢাল
কোনো সরলরেখা বাম থেকে ডান দিকে নিম্নগামী হলেও একই সূত্র দ্বারা সেই রেখার ঢাল নির্ণয় করা যায়। ধরা যাক, AB একটি নিম্নগামী সরলরেখা। যা একমাত্রার চাহিদা অপেক্ষক Y = a- bx হতে অঙ্কন করা হয়েছে। এখন AB সরলরেখার ঢাল নির্ণয় করতে হবে।
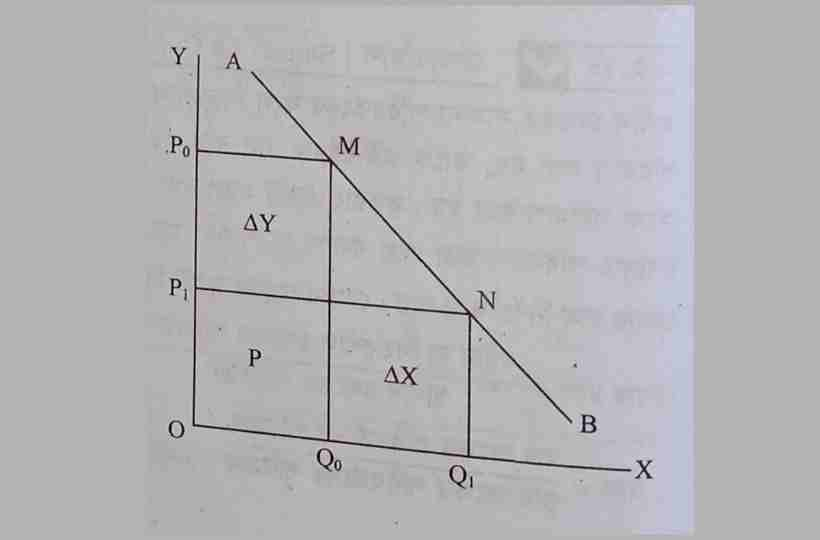
মনে করি, AB রেখার ওপর M বিন্দুতে X ও Y এর প্রাথমিক পরিমাণ Qo ও Po ছিল। পরবর্তীতে X এর পরিমাণ হ্রাস পেয়ে যথাক্রমে Q₁ ও P₁ হয়, যা N বিন্দুতে দেখানো হয়েছে। এখানে AB রেখার উপরিস্থিত M ও N বিন্দুদ্বয়ের স্থানাঙ্ক (Qo. Po) এবং (Q₁, P₁) হয়।
এখানে, ΔX = PN
এবং ΔY = -PM
∴ A বিন্দুতে ঢাল ΔY/ΔX = -PM/PN < 0
অর্থাৎ, ঋণাত্মক ঢাল পাওয়া যায়।

